Converting 0.63 repeating into simplest form fraction

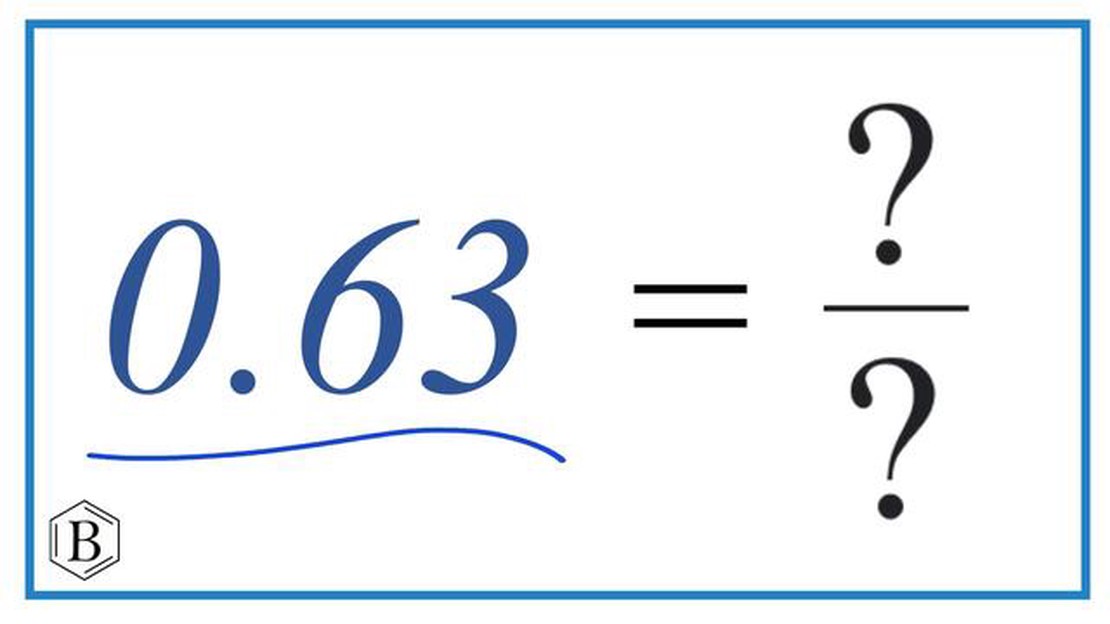
post-thumb

What is 0.63 repeating as a fraction in simplest form?

When it comes to fractions, converting a decimal into its simplest form is a common process that allows us to express the value in a more concise and streamlined format. In this article, we will explore the process of converting the decimal 0.63 repeating into its simplest form fraction.

The decimal 0.63 is a repeating decimal, which means that the digit 63 continues infinitely. To convert this repeating decimal into a fraction, we can use a simple algebraic equation. Let’s represent the repeating decimal as x:

Table Of Contents

x = 0.636363…

To eliminate the repeating part, we can multiply both sides of the equation by a power of 10, which will shift the decimal point to the right:

100x = 63.636363…

Now, we can subtract the original equation from the modified equation to eliminate the repeating part:

100x - x = 63.636363… - 0.636363…

Simplifying the equation gives us:

99x = 63

Dividing both sides of the equation by 99 gives us the simplest form of the fraction:

x = 63/99

Therefore, the simplest form of the repeating decimal 0.63 is 63/99.

Converting decimals into fractions allows us to express values in a more precise and concise manner. By understanding the process of converting repeating decimals into fractions, we can simplify complex numbers and better manipulate them in mathematical calculations.

Converting 0.63 repeating into simplest form fraction

To convert the repeating decimal 0.63 into a simplest form fraction, we can use algebraic manipulation. We can start by noticing that the decimal 0.63 can be written as a fraction as 63/100. This is because the digit 6 in the tenths place represents 6/10 or 60/100, and the digit 3 in the hundredths place represents 3/100. Therefore, 0.63 can be expressed as 63/100.

Now, to simplify this fraction further, we need to find the greatest common divisor (GCD) of the numerator and denominator. In this case, both 63 and 100 can be divided by 7. Therefore, the GCD is 7. By dividing both the numerator and denominator by 7, we get the simplified fraction:

0.63 = 63/100 = (63 ÷ 7)/(100 ÷ 7) = 9/14

Therefore, the simplest form of the repeating decimal 0.63 is 9/14.

It is important to note that when converting repeating decimals into fractions, the process may not always result in a simple fraction. Some repeating decimals may require more complex algebraic techniques, such as setting up equations and solving for variables. However, in this case, we were able to express 0.63 as a simple fraction without any complex calculations.

Gaming

Gaming has become a popular form of entertainment for people of all ages. It provides a way to escape reality and immerse oneself in virtual worlds filled with adventure, strategy, and excitement. Whether playing solo or with friends, gaming offers a multitude of experiences and challenges.

One of the most popular gaming platforms is PC gaming. With its powerful hardware and extensive game library, PC gaming offers a diverse range of genres and titles to choose from. From intense first-person shooters to immersive role-playing games, there is something for every gamer on the PC platform.

In recent years, mobile gaming has also gained significant traction. With the advancement of smartphones and tablets, gamers can now enjoy their favorite games on the go. From casual puzzle games to high-octane racing games, mobile gaming offers a convenient and accessible gaming experience for players of all skill levels.

Multiplayer gaming has also become a staple in the gaming industry. With the rise of online connectivity, gamers can now connect with friends and strangers from around the world to compete or cooperate in various game modes. This social aspect of gaming enhances the overall experience and fosters a sense of community among players.

Gaming technology continues to evolve, pushing the boundaries of what is possible in the virtual realm. From virtual reality to augmented reality, gamers can now immerse themselves in more realistic and interactive gaming experiences. These advancements in technology further enhance the immersion and engagement of players, making gaming an even more captivating form of entertainment.

Read Also: How Many Shots Does It Take to Get Drunk?

General

In general, gaming has become a popular form of entertainment for people of all ages. With the advancement of technology, video games have evolved significantly, providing immersive experiences and captivating storylines. The industry has seen exponential growth in recent years, with new consoles and games being released regularly.

One aspect of gaming that has gained attention is the competitive scene. Esports, or electronic sports, have become a booming industry, with professional gamers competing in tournaments for large prize pools. Games such as League of Legends, Counter-Strike: Global Offensive, and Dota 2 have attracted a massive following and have become major spectator sports.

The gaming community is known for its passion and dedication. Gamers often spend hours honing their skills and exploring virtual worlds. Multiplayer games offer a social aspect, allowing players to connect and play together from different parts of the world. This has created a sense of camaraderie among gamers and has led to the formation of online communities and forums.

In terms of news, gaming outlets provide updates on new game releases, reviews, and industry developments. Gaming conventions, such as E3 and Gamescom, are highly anticipated events where companies showcase their latest projects. These events generate a lot of buzz and excitement among gamers, who eagerly await announcements and trailers for upcoming games.

Overall, gaming has become a significant part of modern culture. It offers a form of escapism and allows individuals to immerse themselves in interactive digital worlds. Whether it’s playing casually for fun or pursuing gaming as a professional career, the general appeal of gaming continues to grow worldwide.

News

New Game Release: The highly anticipated game “Dragon’s Lair 2” is set to be released next month. This sequel to the popular fantasy adventure game promises even more epic quests and challenging puzzles for players to solve. Fans of the original game are excited to see how the story continues and what new features and characters will be introduced.

Read Also: Steph Curry's Overall Rating in NBA 2K17

Gaming Convention Announcement: The annual gaming convention, GameFest, has announced its dates for this year. Gaming enthusiasts from all over the world will gather in the city for three days of non-stop gaming fun. Attendees can expect to try out the latest game releases, participate in gaming tournaments, and meet their favorite game developers and streamers. It’s an event not to be missed!

New Gaming Hardware: A leading tech company has unveiled its latest gaming console, the GameMaster X. Packed with powerful hardware and innovative features, this console aims to revolutionize the gaming experience. With its advanced graphics capabilities and immersive virtual reality support, players can expect to be transported to a whole new level of gaming realism.

Esports Championship: The finals of the highly competitive esports championship, the Legends League, will take place next week. The world’s top esports teams will battle it out in intense matches to claim the title of champions. Fans eagerly await to see which team will emerge victorious and be crowned the best in the world.

  • New Game Release: “Dragon’s Lair 2”
  • Gaming Convention Announcement: GameFest
  • New Gaming Hardware: GameMaster X
  • Esports Championship: Legends League
DateEvent
Next monthNew Game Release: “Dragon’s Lair 2”
TBDGaming Convention Announcement: GameFest
N/ANew Gaming Hardware: GameMaster X
Next weekEsports Championship: Legends League

Stay tuned for more exciting news in the gaming world!

Calculation

In mathematics, calculations are the process of performing mathematical operations to solve a problem or find a result. One example of a calculation is converting a repeating decimal into a simplest form fraction. Let’s consider the decimal 0.63 repeating.

To convert the repeating decimal into a fraction, we can represent it as an infinite geometric series. We start by letting x be the repeating decimal. Next, we multiply both sides of the equation by 100 to move the decimal point two places to the right, obtaining 100x = 63.6363… .

Since the decimal part repeats infinitely, we can express it as a geometric series. By subtracting the equation 100x = 63.6363… from x = 0.6363…, we get 99x = 63 (0.6363… - 0.63 = 0.0063… = 63/10000). Solving for x, we find that x = 63/99.

To simplify the fraction further, we can divide both the numerator and denominator by their greatest common divisor. In this case, the greatest common divisor of 63 and 99 is 9. Dividing both by 9, we get x = 7/11. Therefore, the simplest form fraction equivalent to 0.63 repeating is 7/11.

In summary, the calculation involved converting the repeating decimal 0.63 into a simplest form fraction. This was achieved by representing the decimal as an infinite geometric series and solving for the repeating part. After simplifying the resulting fraction, we found that 0.63 repeating is equivalent to 7/11.

Method

To convert a repeating decimal into simplest form fraction, you need to follow a specific method. First, identify the repeating portion of the decimal. In this case, the repeating portion is 63. To represent this repeating decimal as a fraction, assign a variable to the repeating portion, for example, let’s call it “x”.

Next, multiply both sides of the equation by a power of 10 that shifts the decimal point to the right of the repeating portion. Since the repeating portion has two digits, we multiply both sides by 10^2 (which is 100). This gives us the equation 100x = 63.6363… (where the digit 63 repeats).

Now, subtract the original equation from the multiplied equation to eliminate the repeating portion. We have 100x - x = 63 - 0.63 (the repeating portion divided by 10 to shift the decimal point). Simplifying this equation gives us 99x = 62.37.

To isolate the variable x, divide both sides of the equation by 99. This yields x = 62.37 / 99. Now, we need to simplify this fraction to its simplest form. In this case, the numerator is 62.37 and the denominator is 99.

To simplify the fraction, we need to find the greatest common divisor (GCD) between the numerator and denominator. In this case, the GCD of 62.37 and 99 is 9. Therefore, we can divide both the numerator and denominator by 9 to simplify the fraction.

Dividing 62.37 by 9 gives us approximately 6.93, and dividing 99 by 9 gives us 11. Therefore, the simplest form of the repeating decimal 0.63 is 6.93/11. This fraction cannot be further simplified because 6.93 and 11 do not have a common factor other than 1.

FAQ:

How do I convert 0.63 repeating into a fraction?

To convert 0.63 repeating into a fraction, you can use algebraic manipulation. Let x be equal to 0.63 repeating. Multiply both sides of the equation by 100 to get 100x = 63.333…, and subtract x from both sides to get 99x = 63. This simplifies to x = 63/99. Therefore, the fraction equivalent of 0.63 repeating is 63/99.

Can you explain how to convert 0.63 repeating into simplest form fraction?

Sure! To convert 0.63 repeating into simplest form fraction, you can follow these steps: 1. Let x be equal to 0.63 repeating. 2. Multiply both sides of the equation by 100 to get 100x = 63.333…. 3. Subtract x from both sides to get 99x = 63. 4. Divide both sides by 99 to simplify the fraction. 5. The final result is x = 63/99. However, to express the fraction in simplest form, you can reduce it by dividing both the numerator and denominator by their greatest common divisor. In this case, the greatest common divisor of 63 and 99 is 9. Therefore, 63/99 simplifies to 7/11. So, the simplest form fraction equivalent of 0.63 repeating is 7/11.

What is the easiest way to convert 0.63 repeating into a fraction?

The easiest way to convert 0.63 repeating into a fraction is to recognize the repeating decimal pattern. Since the decimal part is 0.63 repeating, we can represent it as 0.636363… The repeating part can be denoted as x. So, we have the equation x = 0.636363… If we multiply both sides of the equation by 100, we get 100x = 63.636363… Subtracting the original equation x = 0.636363… from 100x = 63.636363…, we get 99x = 63. Dividing both sides of the equation by 99, we get x = 63/99. Therefore, the simplest form fraction equivalent of 0.63 repeating is 63/99.

Is there a method to convert 0.63 repeating into a fraction without algebra?

Yes, there is a method to convert 0.63 repeating into a fraction without algebra. One way is to identify the repeating pattern by observing the decimal representation. In this case, the decimal pattern repeats every two digits, so we can represent it as 0.636363… To convert this into a fraction, we can denote the repeating part (63) as x. Subtracting x from 100x, we get 99x = 63. Dividing both sides by 99, we simplify the fraction to x = 63/99. Therefore, the simplest form fraction equivalent of 0.63 repeating is 63/99.

What is the denominator of the fraction equivalent to 0.63 repeating?

In the fraction equivalent of 0.63 repeating, the denominator is 99. To convert the repeating decimal 0.63 into a fraction, we can represent it as 0.636363… The repeating part (63) can be denoted as x. By subtracting x from 100x, we get 99x = 63, which simplifies to x = 63/99. Therefore, the fraction equivalent of 0.63 repeating has a denominator of 99.

See Also:

    comments powered by Disqus

    You May Also Like