Egy kúpnak 1 vagy 2 oldala van?

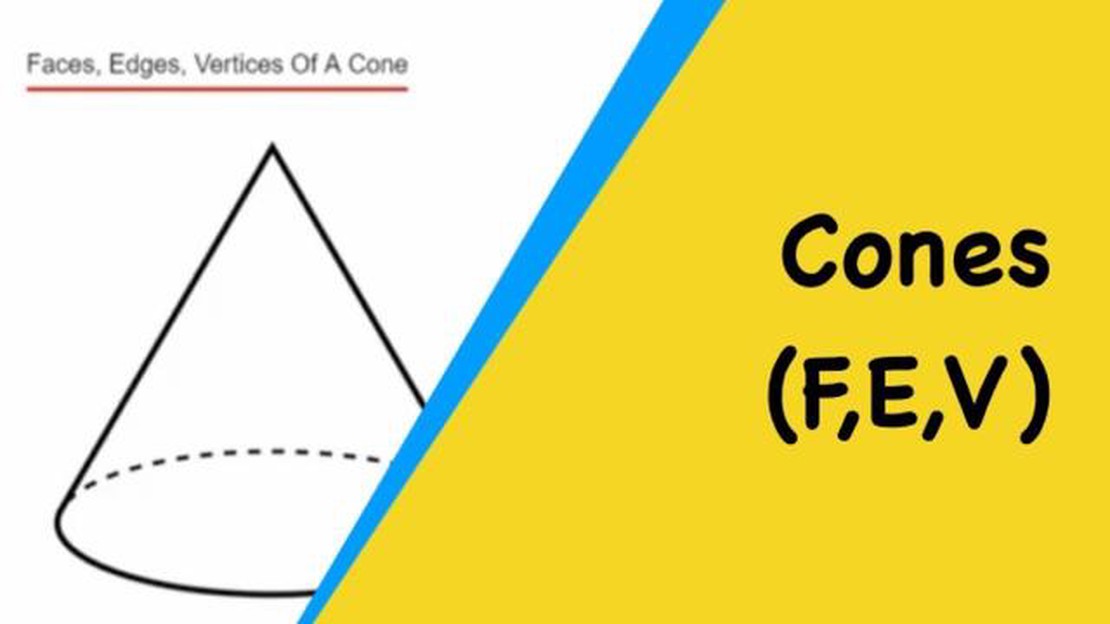
A geometria világában az alakzatok és alakzatok osztályozása gyakran vita tárgyát képezi. Konkrétan az a kérdés, hogy hány oldala van egy kúpnak, vita tárgyát képezi. Egy vagy két oldala van?

Első pillantásra úgy tűnhet, hogy a kúpnak csak egy arca van. Hiszen egyetlen görbült felülete van, amely egy pontba szűkül, és egy partysapkára emlékeztet. Közelebbről megvizsgálva azonban kiderül, hogy a kúpnak valójában két különálló arca van - az ívelt felület és a kör alakú alap.

Az ívelt felület adja a kúp jellegzetes alakját. Az alaptól a csúcsig terjed, és egy összefüggő felületet alkot. Ezt a felületet gyakran nevezik a kúp oldalfelületének vagy oldalfelületének. Fontos megjegyezni, hogy az ívelt felület nem foglalja magában az alapot vagy a csúcsot.

A kúp alapja egy lapos, kör alakú felület, amely az alakzat alját képezi. Ez merőleges a kúp tengelyére, és ez teszi lehetővé, hogy az alakzat egyenesen álljon. Az alap biztosítja a stabilitást, és a kúp alapjaként szolgál. Bár gyakran figyelmen kívül hagyják, az alap valójában a kúp egyik oldala.

Összefoglalva, a kúpnak két különálló oldala van - az ívelt felület és a kör alakú alap. Mindkét oldal hozzájárul a kúp általános alakjához és szerkezetéhez. Míg az ívelt felület a kúp meghatározó jellemzője, az alap ugyanolyan fontos a stabilitás és a tartás szempontjából. Ha tehát legközelebb találkozol egy kúppal, ne feledd, hogy nem csak egy, hanem két oldala van!

Játékhírek: A kúpnak 1 vagy 2 oldala van?

A játékosok vitatkoznak arról, hogy a videojátékokban egy kúpnak egy vagy két arca van. Ez triviális kérdésnek tűnhet, de heves vitát váltott ki a játékrajongók körében.

A vita egyik oldalán azok állnak, akik szerint a kúpnak két arca van. Szerintük a kúp egy görbült felületből és egy kör alakú alapból áll, ami kétarcúvá teszi a tárgyat. Ezt a nézőpontot támasztja alá az a tény, hogy a videojátékokban a kúpokat gyakran két különböző felülettel ábrázolják.

A vita másik oldalán azok a játékosok állnak, akik szerint a kúpnak csak egy arca van. Rámutatnak arra, hogy matematikai értelemben a kúp egy háromdimenziós objektum, amelynek egyetlen görbült felülete van. Ezért úgy vélik, hogy a videojátékokban a kúpot csak egy arculattal kellene ábrázolni.

Bár a vita triviálisnak tűnhet, rávilágít a részletekre és a pontosságra való odafigyelésre, amelyet a játékosok elvárnak a virtuális világoktól. Az a kérdés, hogy hány arca van egy kúpnak, jelentéktelennek tűnhet, de fontos kérdéseket vet fel a tárgyak játékkörnyezetekben való ábrázolásával kapcsolatban.

Végső soron a válasz arra, hogy egy kúpnak egy vagy két arca van-e, a kontextustól és az értelmezéstől függően változhat. A játékfejlesztőkön és -tervezőkön múlik, hogy a matematikai definíciókat és a vizuális esztétikát egyaránt figyelembe véve hogyan kívánnak kúpokat ábrázolni a játékaikban.

Ahogy a játékipar tovább fejlődik, valószínű, hogy az ehhez hasonló viták továbbra is felmerülnek majd. Legyen szó akár arról, hogy hány arca van egy kúpnak, akár a tárgyak kölcsönhatásának fizikájáról, a játékosok mindig válaszokat keresnek, és feszegetik a virtuális valóság határait.

A kúpok geometriájának megértése a játékban

A játékok világában a kúpok döntő szerepet játszanak a magával ragadó és valósághű környezetek létrehozásában. A kúpok geometriájának megértése elengedhetetlen a játékfejlesztők számára a fény és az árnyék pontos ábrázolásához, valamint a lövedékek és más vizuális effektusok viselkedésének szimulálásához.

A kúp egy háromdimenziós geometriai alakzat, amelynek kör alakú alapja és görbe felülete egyetlen pontba, a csúcsba torkollik. A játékokban a kúpokat gyakran használják a karakterek vagy tárgyak látómezejének ábrázolására, például zseblámpák, keresőfények vagy varázslatos effektusok esetében.

A kúp alakja a vizuális effektusok széles skáláját teszi lehetővé a játékokban. Egy kúp alakú fénysugár például dinamikus és valósághű árnyékok létrehozására használható egy 3D-s környezetben. A kúp szögének és hosszának beállításával a fejlesztők szabályozhatják a fény terjedését és intenzitását, így az természetesebbnek és magával ragadóbbnak tűnik.

A vizuális hatások létrehozása mellett a kúpok a lövedékek vagy más tárgyak viselkedésének szimulálására is használhatók a játékokban. Például amikor egy karakter eldob egy gránátot vagy kilő egy lövedéket, a tárgy röppályáját kúppal lehet ábrázolni. A kúp méretének és szögének beállításával a fejlesztők pontosan ábrázolhatják az objektum útját és hatótávolságát, ami egy réteg realizmussal gazdagítja a játékmenetet.

A kúpok geometriájának megértése a játékokban elengedhetetlen a vizuálisan vonzó és magával ragadó élmények létrehozásához. Akár a valósághű megvilágítás szimulálásáról, akár a lövedékek viselkedésének pontos ábrázolásáról van szó, a kúpok olyan sokoldalú eszköz, amelyre a játékfejlesztők támaszkodnak a virtuális világok életre keltéséhez.

A vita: 1 arc vagy 2 arc?

A vita arról, hogy egy kúpnak egy vagy két arca van-e, évek óta vita tárgya a matematikusok és a geometria szerelmesei között. A kérdésre adott válasz attól függ, hogyan definiáljuk az arcot, és hogyan értelmezzük a kúp alakját.

Egyesek azt állítják, hogy a kúpnak csak egy arca van, mivel háromdimenziós tárgy, amely görbe, és nincsenek különálló oldalai. Úgy vélik, hogy mivel az arcot általában sík felületnek tekintik, a kúpnak nem lehet több arca. Ezt az álláspontot támasztja alá az a tény, hogy a kúp egyetlen sík felületet alkotva kibontható.

Másrészt vannak olyanok, akik azt állítják, hogy a kúpnak két oldala van. Ők azzal érvelnek, hogy egy felületet úgy is lehet definiálni, mint egy tárgy határát vagy határkomponensét. Ebben az értelmezésben a kúp ívelt felületét tekintik az egyik oldalnak, míg a kúp kör alakú alapját egy másik oldalnak. Azt állítják, hogy csak azért, mert egy felület görbült és nem sík, még nem jelenti azt, hogy különálló felületként kell kezelni.

Olvassa el továbbá: Miért a legjobb, hogy elkerülje Squishing százlábúak

A vitát tovább bonyolítja, hogy egyes matematikusok szerint a kúpnak végtelen számú arca lehet. Azzal érvelnek, hogy ahogy a kúp magassága a nulla felé csökken, az oldalak száma végtelenül megnő. Ez a nézőpont figyelembe veszi a kúp változó keresztmetszetét, ahogy a csúcs felé keskenyedik.

Összefoglalva, a vita arról, hogy egy kúpnak egy vagy két oldala van-e, nézőpont és értelmezés kérdése. Attól függ, hogyan definiáljuk az arcot, és hogyan tekintjük a kúp görbült felületét és alapját. Végső soron mindkét érvnek van létjogosultsága, és a válasz attól függően változhat, hogy a kérdés milyen kontextusban hangzik el.

Szakértői vélemények a kúpok arcának számáról

Amikor arról van szó, hogy egy kúpnak hány arca van, a terület szakértői között vita van. Bár sokan azt feltételezik, hogy a kúpnak csak egy arca van - az ívelt felület -, vannak érvek amellett, hogy a kúpnak két arca van.

Az egyik nézet szerint a kúpnak két oldala van, mivel van egy teteje és egy alja. Ez a nézet a kúp alját különálló, a görbült felülettől elkülönülő oldalnak tekinti. E nézőpont szerint a kúp két síkbeli felületből álló háromdimenziós tárgynak tekinthető.

Másrészt egyes szakértők szerint a kúpot úgy kell besorolni, mint amelynek csak egy oldala van. Azzal érvelnek, hogy a kúp görbült felülete folytonos, és nincsenek határozott élei vagy sarkai, így lényegében egyetlen oldala van. Ez a nézőpont a kúp felületének sima, folytonos jellegét hangsúlyozza.

Végső soron a vita arról, hogy egy kúpnak hány arca van, értelmezési kérdésnek tekinthető, és annak, hogy a háromdimenziós geometria kontextusában hogyan definiáljuk az “arcot”. Míg egyesek inkább úgy tekintik, hogy a kúpnak két oldala van, mások szerint csak egy. Ez a véleménykülönbség rávilágít a geometria területén belüli nézőpontok összetettségére és sokféleségére.

Olvassa el továbbá: A tökéletes kormánykerék kiválasztása az American Truck Simulatorhoz

Következmények a játékmechanikára és a grafikára nézve

A kúp oldalainak számának megértése jelentős hatással van a játékmechanikára és a grafikára.

Amikor háromdimenziós objektumok megjelenítéséről van szó egy videojátékban, a kúpokat gyakran használják különböző struktúrák vagy objektumok ábrázolására. Ha egy kúpot úgy definiálnánk, hogy csak egy arca van, az korlátozná a fejlesztők lehetőségeit az ilyen objektumok létrehozására és manipulálására.

Ha például a tervezők és fejlesztők azt az értelmezést követnék, hogy a kúpnak csak egy arca van, az korlátozná őket abban, hogy bonyolult részleteket vagy textúrát adjanak a kúpos objektum felületéhez. Ez a korlátozás potenciálisan hatással lehet a játék általános vizuális vonzerejére és realizmusára.

Másrészt, ha a kúpnak két oldala van, akkor több lehetőség nyílik a játéktervezők számára, hogy összetett kúpszerű formákat hozzanak létre, például kettős kúpot vagy lyukas kúpot a közepén. Ez a rugalmasság dinamikusabb játékmechanikát és vizuálisan vonzó grafikát tesz lehetővé.

Ráadásul a következmények túlmutatnak a grafikán. A játékmechanika, például az ütközésérzékelés, a fizikai szimulációk és a tárgyak kölcsönhatásai a játékvilágban lévő tárgyak geometriájának pontos meghatározására támaszkodnak. Ha egy kúpnak több arca van, akkor a fejlesztőknek kifinomultabb algoritmusokat kell kifejleszteniük és megvalósítaniuk a kúpok egyedi tulajdonságainak kezelésére.

Összefoglalva, annak értelmezése, hogy egy kúpnak hány arca van, hatással van a vizuálisan vonzó grafika és dinamikus játékmechanika létrehozásának lehetőségeire. Akár úgy tekintjük, hogy egy kúpnak egy, akár két arca van, a játékfejlesztők számára alapvető fontosságú, hogy megértsék és megfelelően alkalmazzák ezt a koncepciót, hogy magával ragadó és élvezetes játékélményt teremtsenek.

A kúpgeometria jövőbeli fejlesztései

A kúpgeometria a matematikusok és a mérnökök számára egyaránt fontos kutatási terület. Míg a kúpok alapvető tulajdonságai és képletei jól ismertek, a folyamatban lévő kutatások izgalmas jövőbeli fejlesztésekhez vezetnek ezen a területen.

A kúpgeometria jövőbeli fejlesztéseinek egyik fókuszterülete a magasabb dimenziós kúpok vizsgálata. Míg a hagyományos kúp háromdimenziós, a kutatók azt vizsgálják, hogyan lehet a kúpok tulajdonságait négy vagy még magasabb dimenzióra kiterjeszteni. Ez fontos következményekkel jár az olyan területeken történő alkalmazásokra, mint a számítógépes grafika és a fizika.

Egy másik érdekes terület a nem hagyományos kúpok tanulmányozása. Míg a legismertebb kúpforma a derékszögű kör alakú kúp, a kutatók különböző típusú görbéket vizsgálnak, amelyek egy kúp alapját képezhetik. Ez új lehetőségeket nyit meg a kúpgeometria megértésére és alkalmazására különböző összefüggésekben.

A számítási módszerek fejlődése szintén szerepet játszik a kúpgeometria jövőjében. A számítógépek teljesítményének növekedésével a kutatók gyorsabban és pontosabban tudják elvégezni a kúpokkal kapcsolatos összetett számításokat és szimulációkat. Ez lehetővé teszi a kúpgeometria részletesebb feltárását, és új felfedezésekre ad lehetőséget.

Emellett a kúpgeometria alkalmazása a valós életben is folyamatos kutatás tárgyát képezi. A kúpok tulajdonságainak megértése fontos az olyan területeken, mint az építészet, a mérnöki tudományok és a fizika. A kúpgeometria további feltárásával a kutatók hatékonyabb terveket és megoldásokat dolgozhatnak ki valós problémákra.

Összefoglalva, a kúpgeometria jövőbeli fejlesztései nagy ígéretet hordoznak e fontos matematikai fogalom megértésének bővítésére. A magasabb dimenziós kúpok feltárásától a nem hagyományos kúpformák tanulmányozásáig ezek a fejlesztések hatással lehetnek különböző területekre, és új előrelépésekhez vezethetnek a technológia és a tervezés terén.

GYIK:

Hány oldala van egy kúpnak?

A kúpnak két oldala van - egy kör alakú alap és egy ívelt oldalfelület.

Lehet egy kúpnak egy arca?

Nem, egy kúpnak nem lehet csak egy arca. Egy kör alakú alappal és egy ívelt oldalsó felülettel kell rendelkeznie, tehát két oldala van.

Milyen oldalai vannak a kúpnak?

A kúp oldalai a kör alakú alap és az ívelt oldalfelület.

A kúp kör alakú alja is arcnak tekinthető?

Igen, a kúp kör alakú alapját a kúp egyik oldalának tekintjük.

Miért tekinthető a kúpnak két oldala van?

A kúpnak két oldala van, mert a kúpnak van egy kör alakú alapja és egy ívelt oldalsó felülete, amelyek együttesen alkotják a kúp két oldalát.

Egyenlő méretű-e a kúp két oldala?

Nem, a kúp két oldala nem egyenlő méretű. A kör alakú alap jellemzően nagyobb méretű, mint az ívelt oldalfelület.

Lásd még:

• Hogyan lehet leleplezni az Attika kőbánya kultista
• Ki adja Aloy hangját a Genshin Impactben?
• A legjobb csapatösszeállítások a Baal számára: Fedezd fel a végső szinergiákat
• Mi a helyzet? A pillanat legforróbb videojátéka
• Natalie Teeger megköti a csomót?
• Az Elemi Mesteri Erők megértése a Genshin Impactben
• Mi a végső ingyenes rejtett tárgy játék?