Konwersja 0,63 powtórzenia na ułamek zwykły

Ile wynosi 0,63 powtarzające się jako ułamek w najprostszej postaci?

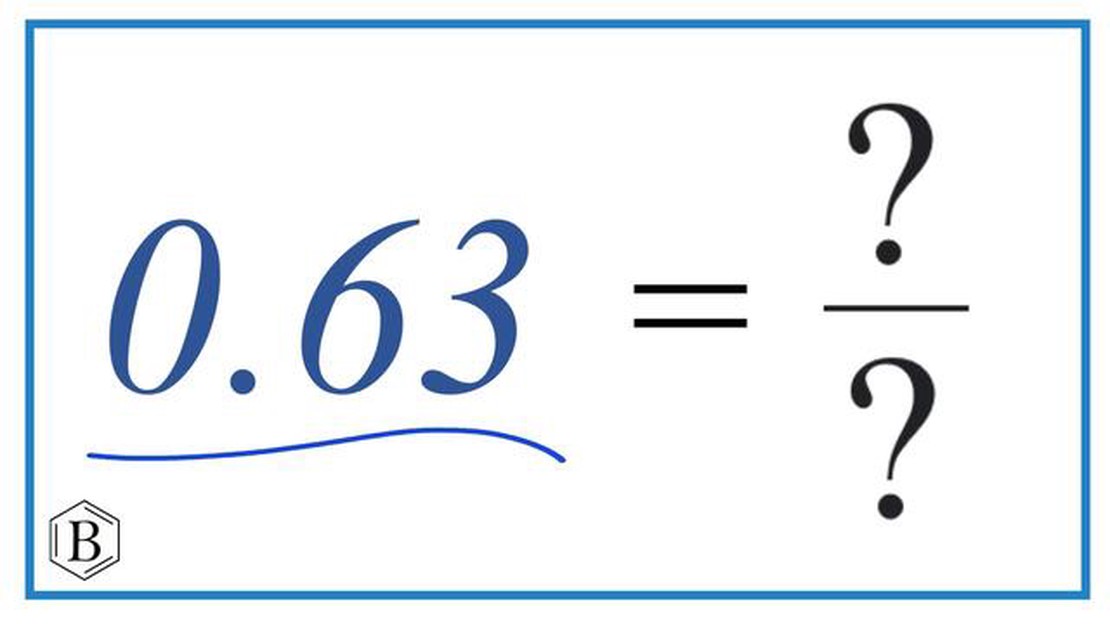
Jeśli chodzi o ułamki, konwersja ułamka dziesiętnego do jego najprostszej postaci jest powszechnym procesem, który pozwala nam wyrazić wartość w bardziej zwięzłym i uproszczonym formacie. W tym artykule przeanalizujemy proces konwersji ułamka dziesiętnego 0,63 powtarzającego się do jego najprostszej postaci.

Spis treści

Liczba dziesiętna 0,63 jest liczbą dziesiętną powtarzającą się, co oznacza, że cyfra 63 jest nieskończona. Aby przekształcić tę powtarzającą się liczbę dziesiętną w ułamek, możemy użyć prostego równania algebraicznego. Przedstawmy powtarzającą się liczbę dziesiętną jako x:

x = 0.636363…

Aby wyeliminować powtarzającą się część, możemy pomnożyć obie strony równania przez potęgę 10, co spowoduje przesunięcie przecinka dziesiętnego w prawo:

100x = 63.636363…

Teraz możemy odjąć oryginalne równanie od zmodyfikowanego równania, aby wyeliminować powtarzającą się część:

100x - x = 63.636363… - 0.636363…

Upraszczając równanie otrzymujemy:

99x = 63

Dzieląc obie strony równania przez 99 otrzymujemy najprostszą postać ułamka:

x = 63/99

Zatem najprostszą formą powtarzającego się ułamka dziesiętnego 0,63 jest 63/99.

Konwersja ułamków dziesiętnych na ułamki pozwala nam wyrażać wartości w bardziej precyzyjny i zwięzły sposób. Rozumiejąc proces konwersji powtarzających się ułamków dziesiętnych na ułamki, możemy uprościć złożone liczby i lepiej nimi manipulować w obliczeniach matematycznych.

Konwersja 0,63 powtarzającego się ułamka dziesiętnego na ułamek zwykły

Aby przekształcić powtarzającą się liczbę dziesiętną 0,63 w ułamek zwykły, możemy użyć manipulacji algebraicznych. Możemy zacząć od zauważenia, że ułamek dziesiętny 0,63 może być zapisany jako ułamek 63/100. Dzieje się tak, ponieważ cyfra 6 na miejscu dziesiątym reprezentuje 6/10 lub 60/100, a cyfra 3 na miejscu setnym reprezentuje 3/100. Dlatego 0,63 można wyrazić jako 63/100.

Teraz, aby jeszcze bardziej uprościć ten ułamek, musimy znaleźć największy wspólny dzielnik (GCD) licznika i mianownika. W tym przypadku zarówno 63, jak i 100 można podzielić przez 7. Dlatego GCD wynosi 7. Dzieląc zarówno licznik, jak i mianownik przez 7, otrzymujemy uproszczony ułamek:

0.63 = 63/100 = (63 ÷ 7)/(100 ÷ 7) = 9/14

Zatem najprostszą formą powtarzającego się ułamka dziesiętnego 0,63 jest 9/14.

Ważne jest, aby pamiętać, że podczas przekształcania powtarzających się ułamków dziesiętnych w ułamki, proces ten nie zawsze prowadzi do uzyskania ułamka zwykłego. Niektóre powtarzające się ułamki dziesiętne mogą wymagać bardziej złożonych technik algebraicznych, takich jak tworzenie równań i rozwiązywanie zmiennych. Jednak w tym przypadku byliśmy w stanie wyrazić 0,63 jako ułamek zwykły bez żadnych skomplikowanych obliczeń.

Rozgrywka

Gry stały się popularną formą rozrywki dla ludzi w każdym wieku. Zapewnia sposób na ucieczkę od rzeczywistości i zanurzenie się w wirtualnych światach pełnych przygód, strategii i emocji. Niezależnie od tego, czy grasz solo, czy z przyjaciółmi, gry oferują wiele doświadczeń i wyzwań.

Jedną z najpopularniejszych platform do grania jest PC. Dzięki potężnemu sprzętowi i obszernej bibliotece gier, gry na PC oferują szeroki wybór gatunków i tytułów do wyboru. Od intensywnych strzelanek pierwszoosobowych po wciągające gry fabularne - na platformie PC każdy gracz znajdzie coś dla siebie.

W ostatnich latach gry mobilne również zyskały na popularności. Wraz z rozwojem smartfonów i tabletów, gracze mogą teraz cieszyć się swoimi ulubionymi grami w podróży. Od zwykłych gier logicznych po wysokooktanowe gry wyścigowe, gry mobilne oferują wygodne i dostępne wrażenia z gry dla graczy na wszystkich poziomach umiejętności.

Gry wieloosobowe stały się również podstawą w branży gier. Wraz z rozwojem łączności online, gracze mogą teraz łączyć się z przyjaciółmi i nieznajomymi z całego świata, aby rywalizować lub współpracować w różnych trybach gry. Ten społeczny aspekt gier poprawia ogólne wrażenia i sprzyja poczuciu wspólnoty wśród graczy.

Technologia gier wciąż ewoluuje, przesuwając granice tego, co jest możliwe w wirtualnym świecie. Od wirtualnej rzeczywistości po rzeczywistość rozszerzoną, gracze mogą teraz zanurzyć się w bardziej realistycznych i interaktywnych grach. Te postępy technologiczne jeszcze bardziej zwiększają immersję i zaangażowanie graczy, czyniąc gry jeszcze bardziej wciągającą formą rozrywki.

Ogólne

Ogólnie rzecz biorąc, gry stały się popularną formą rozrywki dla osób w każdym wieku. Wraz z rozwojem technologii, gry wideo znacznie ewoluowały, zapewniając wciągające wrażenia i wciągającą fabułę. W ostatnich latach branża odnotowała gwałtowny wzrost, a nowe konsole i gry są regularnie wydawane.

Czytaj także: Jaki poziom można osiągnąć w WoW?

Jednym z aspektów gier, który zyskał uwagę, jest scena rywalizacji. Esport, czyli sporty elektroniczne, stały się dynamicznie rozwijającą się branżą, w której profesjonalni gracze rywalizują w turniejach o duże pule nagród. Gry takie jak League of Legends, Counter-Strike: Global Offensive i Dota 2 przyciągnęły ogromną rzeszę fanów i stały się głównymi sportami widowiskowymi.

Społeczność graczy znana jest ze swojej pasji i poświęcenia. Gracze często spędzają godziny na doskonaleniu swoich umiejętności i odkrywaniu wirtualnych światów. Gry wieloosobowe oferują aspekt społeczny, pozwalając graczom łączyć się i grać razem z różnych części świata. Stworzyło to poczucie koleżeństwa wśród graczy i doprowadziło do powstania społeczności i forów internetowych.

Jeśli chodzi o wiadomości, sklepy z grami dostarczają aktualizacji na temat nowych wydań gier, recenzji i rozwoju branży. Konwencje gamingowe, takie jak E3 i Gamescom, to bardzo oczekiwane wydarzenia, na których firmy prezentują swoje najnowsze projekty. Wydarzenia te generują wiele szumu i ekscytacji wśród graczy, którzy z niecierpliwością czekają na zapowiedzi i zwiastuny nadchodzących gier.

Ogólnie rzecz biorąc, gry stały się istotną częścią współczesnej kultury. Oferuje formę eskapizmu i pozwala jednostkom zanurzyć się w interaktywnych cyfrowych światach. Niezależnie od tego, czy gra się od niechcenia dla zabawy, czy też robi się z tego karierę zawodową, ogólna atrakcyjność gier wciąż rośnie na całym świecie.

Czytaj także: Czy możliwe jest zwiększenie limitu mebli w Genshin?

Aktualności

Premiera nowej gry: Bardzo oczekiwana gra “Dragon’s Lair 2” zostanie wydana w przyszłym miesiącu. Ta kontynuacja popularnej gry przygodowej fantasy obiecuje jeszcze więcej epickich zadań i trudnych zagadek do rozwiązania dla graczy. Fani oryginalnej gry są podekscytowani, aby zobaczyć, jak historia będzie kontynuowana i jakie nowe funkcje i postacie zostaną wprowadzone.

Ogłoszenie konwencji gier: Coroczna konwencja gier, GameFest, ogłosiła daty na ten rok. Entuzjaści gier z całego świata zgromadzą się w mieście na trzy dni nieprzerwanej zabawy. Uczestnicy będą mogli wypróbować najnowsze gry, wziąć udział w turniejach i spotkać się z ulubionymi twórcami gier i streamerami. To wydarzenie, którego nie można przegapić!

Nowy sprzęt do gier: Wiodąca firma technologiczna zaprezentowała swoją najnowszą konsolę do gier, GameMaster X. Wyposażona w potężny sprzęt i innowacyjne funkcje, konsola ta ma na celu zrewolucjonizowanie wrażeń z gry. Dzięki zaawansowanym możliwościom graficznym i obsłudze wciągającej rzeczywistości wirtualnej, gracze mogą spodziewać się przeniesienia na zupełnie nowy poziom realizmu rozgrywki.

Mistrzostwa e-sportowe: Finały wysoce konkurencyjnych mistrzostw e-sportowych, Legends League, odbędą się w przyszłym tygodniu. Najlepsze drużyny e-sportowe na świecie zmierzą się w intensywnych meczach, aby zdobyć tytuł mistrzów. Fani z niecierpliwością czekają, aby zobaczyć, która drużyna zwycięży i zostanie uznana za najlepszą na świecie.

Premiera nowej gry: “Dragon’s Lair 2”. Zapowiedź konwentu gier: GameFest
Nowy sprzęt do gier: GameMaster XMistrzostwa sportowe:* Legends League

Data	Wydarzenie
W przyszłym miesiącu premiera nowej gry: “Dragon’s Lair 2”
Ogłoszenie konwentu gier: GameFest
Nowy sprzęt dla graczy: GameMaster X
W przyszłym tygodniu	Mistrzostwa e-sportowe: Legends League

Bądź na bieżąco z kolejnymi ekscytującymi wiadomościami ze świata gier!

Obliczenia

W matematyce obliczenia to proces wykonywania operacji matematycznych w celu rozwiązania problemu lub znalezienia wyniku. Jednym z przykładów obliczeń jest przekształcenie powtarzającej się liczby dziesiętnej w ułamek zwykły. Rozważmy powtarzający się ułamek dziesiętny 0,63.

Aby przekształcić powtarzającą się liczbę dziesiętną na ułamek, możemy przedstawić ją jako nieskończony szereg geometryczny. Zaczynamy od tego, że x jest powtarzającą się liczbą dziesiętną. Następnie mnożymy obie strony równania przez 100, aby przesunąć kropkę dziesiętną o dwa miejsca w prawo, uzyskując 100x = 63,6363… .

Ponieważ część dziesiętna powtarza się w nieskończoność, możemy wyrazić ją jako szereg geometryczny. Odejmując równanie 100x = 63,6363… od x = 0,6363…, otrzymujemy 99x = 63 (0,6363… - 0,63 = 0,0063… = 63/10000). Rozwiązując dla x, stwierdzamy, że x = 63/99.

Aby jeszcze bardziej uprościć ułamek, możemy podzielić zarówno licznik, jak i mianownik przez ich największy wspólny dzielnik. W tym przypadku największym wspólnym dzielnikiem liczb 63 i 99 jest 9. Dzieląc obie liczby przez 9, otrzymujemy x = 7/11. W związku z tym, ułamek w najprostszej postaci odpowiadający 0,63 jest równy 7/11.

Podsumowując, obliczenia polegały na przekształceniu powtarzającego się ułamka dziesiętnego 0,63 w ułamek zwykły. Osiągnięto to poprzez przedstawienie ułamka dziesiętnego jako nieskończonego szeregu geometrycznego i rozwiązanie dla powtarzającej się części. Po uproszczeniu otrzymanego ułamka okazało się, że powtarzające się 0,63 jest równe 7/11.

Metoda

Aby przekonwertować powtarzający się ułamek dziesiętny na ułamek w najprostszej postaci, należy postępować zgodnie z określoną metodą. Najpierw należy zidentyfikować powtarzającą się część ułamka dziesiętnego. W tym przypadku powtarzająca się część to 63. Aby przedstawić tę powtarzającą się część dziesiętną jako ułamek, przypisz zmienną do powtarzającej się części, na przykład nazwijmy ją “x”.

Następnie pomnóż obie strony równania przez potęgę 10, która przesunie kropkę dziesiętną na prawo od powtarzającej się części. Ponieważ powtarzająca się część ma dwie cyfry, mnożymy obie strony przez 10^2 (czyli 100). W ten sposób otrzymujemy równanie 100x = 63,6363… (gdzie cyfra 63 powtarza się).

Teraz odejmujemy oryginalne równanie od pomnożonego równania, aby wyeliminować powtarzającą się część. Mamy 100x - x = 63 - 0,63 (powtarzająca się część podzielona przez 10 w celu przesunięcia przecinka dziesiętnego). Upraszczając to równanie otrzymujemy 99x = 62,37.

Aby wyodrębnić zmienną x, podziel obie strony równania przez 99. W ten sposób otrzymasz x = 62,37 / 99. Teraz musimy uprościć ten ułamek do jego najprostszej postaci. W tym przypadku licznik wynosi 62,37, a mianownik 99.

Aby uprościć ułamek, musimy znaleźć największy wspólny dzielnik (GCD) między licznikiem i mianownikiem. W tym przypadku GCD 62,37 i 99 wynosi 9. Możemy zatem podzielić zarówno licznik, jak i mianownik przez 9, aby uprościć ułamek.

Dzieląc 62,37 przez 9 otrzymamy w przybliżeniu 6,93, a dzieląc 99 przez 9 otrzymamy 11. Dlatego najprostszą formą powtarzającego się ułamka dziesiętnego 0,63 jest 6,93/11. Ułamek ten nie może być dalej upraszczany, ponieważ 6,93 i 11 nie mają wspólnego czynnika innego niż 1.

FAQ:

Jak przekonwertować powtarzające się 0,63 na ułamek?

Aby przekonwertować 0,63 powtarzające się na ułamek, można użyć manipulacji algebraicznej. Niech x będzie równe 0,63 powtórzenia. Pomnóż obie strony równania przez 100, aby otrzymać 100x = 63,333… i odejmij x od obu stron, aby otrzymać 99x = 63. To upraszcza się do x = 63/99. Zatem ułamkowy odpowiednik 0,63 powtarzającego się wynosi 63/99.

Czy możesz wyjaśnić, jak przekonwertować 0,63 powtarzające się na ułamek w najprostszej postaci?

Oczywiście! Aby przekonwertować 0.63 powtarzające się na ułamek w najprostszej postaci, możesz wykonać następujące kroki: 1. Niech x będzie równe 0,63 powtórzenia. 2. Pomnóż obie strony równania przez 100, aby otrzymać 100x = 63.333…. 3. Odejmij x od obu stron, aby otrzymać 99x = 63. 4. Podziel obie strony przez 99, aby uprościć ułamek. 5. Wynik końcowy to x = 63/99. Aby jednak wyrazić ułamek w najprostszej postaci, można go zredukować, dzieląc zarówno licznik, jak i mianownik przez ich największy wspólny dzielnik. W tym przypadku największy wspólny dzielnik liczb 63 i 99 wynosi 9. Dlatego liczba 63/99 upraszcza się do 7/11. Zatem najprostszym odpowiednikiem ułamka 0,63 jest 7/11.

Jaki jest najprostszy sposób przekształcenia liczby 0,63 z powtórzeniami na ułamek?

Najłatwiejszym sposobem konwersji 0,63 powtarzającego się na ułamek jest rozpoznanie powtarzającego się wzoru dziesiętnego. Ponieważ część dziesiętna powtarza się 0,63, możemy przedstawić ją jako 0,636363… Powtarzająca się część może być oznaczona jako x. Mamy więc równanie x = 0,636363…. Jeśli pomnożymy obie strony równania przez 100, otrzymamy 100x = 63,636363… Odejmując pierwotne równanie x = 0,636363… od 100x = 63,636363…, otrzymamy 99x = 63. Dzieląc obie strony równania przez 99, otrzymujemy x = 63/99. Zatem najprostszym odpowiednikiem ułamka powtarzającego się 0,63 jest 63/99.

Czy istnieje metoda konwersji 0,63 powtarzające się na ułamek bez algebry?

Tak, istnieje metoda konwersji 0,63 powtarzającego się na ułamek bez algebry. Jednym ze sposobów jest zidentyfikowanie powtarzającego się wzoru poprzez obserwację reprezentacji dziesiętnej. W tym przypadku wzór dziesiętny powtarza się co dwie cyfry, więc możemy go przedstawić jako 0,636363…. Aby przekształcić to w ułamek, możemy oznaczyć powtarzającą się część (63) jako x. Odejmując x od 100x, otrzymamy 99x = 63. Dzieląc obie strony przez 99, upraszczamy ułamek do x = 63/99. Zatem najprostszym odpowiednikiem ułamka powtarzającego się 0,63 jest ułamek 63/99.

Jaki jest mianownik ułamka równego 0,63 z powtórzeniami?

W ułamkowym równoważniku liczby 0,63, mianownik wynosi 99. Aby przekształcić powtarzającą się liczbę dziesiętną 0,63 na ułamek, możemy przedstawić ją jako 0,636363…. Powtarzająca się część (63) może być oznaczona jako x. Odejmując x od 100x, otrzymujemy 99x = 63, co upraszcza się do x = 63/99. Zatem odpowiednik ułamka powtarzającego się 0,63 ma mianownik 99.